[français]
Image denoising with GGMM patch priors
Description
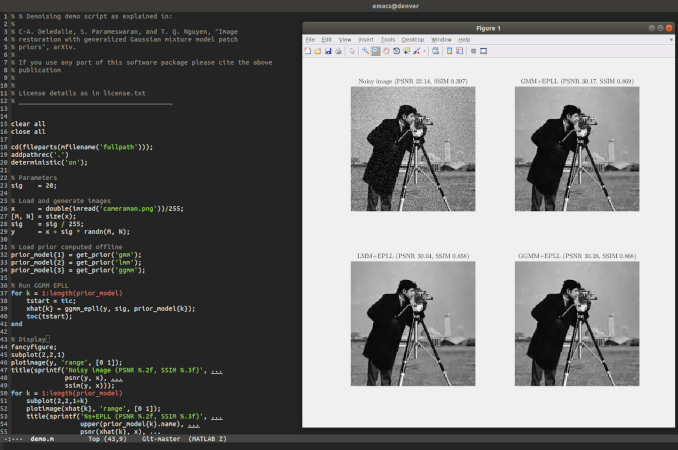Results of GGMM-EPLL
- Patch priors have become an important component of image restoration. A powerful approach in this category of restoration algorithms is the popular Expected Patch Log-Likelihood (EPLL) algorithm. EPLL uses a Gaussian mixture model (GMM) prior learned on clean image patches as a way to regularize degraded patches. In this paper, we show that a generalized Gaussian mixture model (GGMM) captures the underlying distribution of patches better than a GMM. Even though GGMM is a powerful prior to combine with EPLL, the non-Gaussianity of its components presents major challenges to be applied to a computationally intensive process of image restoration. Specifically, each patch has to undergo a patch classification step and a shrinkage step. These two steps can be efficiently solved with a GMM prior but are computationally impractical when using a GGMM prior. In this paper, we provide approximations and computational recipes for fast evaluation of these two steps, so that EPLL can embed a GGMM prior on an image with more than tens of thousands of patches. Our main contribution is to analyze the accuracy of our approximations based on thorough theoretical analysis. Our evaluations indicate that the GGMM prior is consistently a better fit for modeling image patch distribution and performs better on average in image denoising task.
- The goal of this work is to quantify the improvements obtained in image denoising tasks by incorporating a GGMM in EPLL algorithm. Unlike other studies that incorporates a GGMM prior in a posterior mean estimator based on importance sampling, we directly extend the maximum a posteriori formulation of Zoran and Weiss (2011) for the case of GGMM priors. While such a GGMM prior has the ability to capture the underlying distribution of clean patches more closely, we will show that it introduces two major computational challenges in this case. The first one can be thought of as a classification task in which a noisy patch is assigned to one of the components of the mixture. The second one corresponds to an estimation task where a noisy patch is denoised given that it belongs to one of the components of the mixture. Due to the interaction of the noise distribution with the GGD prior, we first show that these two tasks lead to a group of one-dimensional integration and optimization problems, respectively. In general, they do not admit closed-form solutions but some particular solutions or approximations have been derived for the estimation/optimization problem. By contrast, up to our knowledge, little is known for approximating the classification/integration one (only crude approximations were proposed). Our contributions are both theoretical- and application-oriented. The major contribution of this paper, which is and theoretical in nature, is to develop an accurate approximation for the classification/integration problem. In particular, we show that our approximation error vanishes for small and large values of its argument. On top of that, we prove that the two problems enjoy some important desired properties. These theoretical results allow the two quantities to be approximated by functions that can be quickly evaluated in order to be incorporated in fast algorithms. Our last contribution is experimental and concerns the performance evaluation of the proposed model in image denoising scenario.
- Our numerical experiments indicate that our flexible GGMM patch prior is a better fit for modeling natural images than GMM and other mixture distributions with constant shape parameters such as LMM or HLMM. In image denoising tasks, we have shown that using GGMM priors, often, outperforms GMM when used in the EPLL framework. Nevertheless, we believe the performance of GGMM prior in these scenarios falls short of its expected potential. Given that GGMM is persistently a better prior than GMM (in terms of log-likelihood), one would expect the GGMM-EPLL to outperform GMM-EPLL consistently. We postulate that this under-performance is caused by the EPLL strategy that we use for optimization. That is, even though the GGMM prior may be improving the quality of the global solution, the half quadratic splitting strategy used in EPLL is not guaranteed to return a better solution due to the non-convexity of the underlying problem. For this reason, we will focus our future work in designing specific optimization strategies for GGMM-EPLL leveraging the better expressivity of the proposed prior model for denoising and other general restoration applications.
Associated publications and source codes
Associated publications/reports:-
Image denoising with generalized Gaussian mixture model patch priors,
Charles-Alban Deledalle, Shibin Parameswaran, Truong Q. Nguyen
SIAM Journal on Imaging Sciences (in press)
- Download GGMM-EPLL:
- Git:
git clone https://cdeledalle@bitbucket.org/cdeledalle/ggmm-epll.git - Archive: master.zip
- BitBucket: https://bitbucket.org/cdeledalle/ggmm-epll
- Git:
Last modified: Fri Aug 23 13:52:01 UTC 2019