[français]
Charles Deledalle - Teaching
- UCSD ECE285 Machine learning for image processing
- UCSD ECE285 Image and video restoration
- UCSD KPU's Smart IoT Workshop (Summer 2019)
- Miscellaneaous
UCSD ECE285 Machine learning for image processing
Spring 2019 version: click here.
Lectures

|
|
|

|

|
|
Assignments (individual)
- Assignment 0 - Python, Numpy and Matplotlib (prereq, optional)
- Assignment 1 - Backpropagation
- Assignment 2 - CNNs and Pytorch
- Assignment 3 - Transfer Learning
- Assignment 4 - Image Denoising
- MNIST: dataset, MNISTtools.py
- Caltech-UCSD-Birds: dataset, train.csv, val.csv
- BSDS: dataset
- nntools package: nntools.py
Projects (pick only one of them, by groups of 3/4)
- Project A - Image Captioning
- Project B - Style Transfer
- Project C - Multi-Object detection
- Project D - Open-ended
Supplemtary meterials
Everything else
- Fall 2019: enroll to Piazza ECE285 MLIP FA19. Access Google Calendar.
- Spring 2019: enroll to Piazza ECE285 MLIP SP19. Access Google Calendar.
- Fall 2018: enroll to Piazza ECE285 MLIP FA18
- Spring 2018: Go to TritonEd
UCSD ECE285 Image and video restoration
Fall 2017 Matlab version: click here.
Lectures
Image sciences, image processing, image restoration, photo manipulation. Image and videos representation. Digital versus analog imagery. Quantization and sampling. Sources and models of noises in digital CCD imagery: photon, thermal and readout noises. Sources and models of blurs. Convolutions and point spread functions. Overview of other standard models, problems and tasks: salt-and-pepper and impulse noises, half toning, inpainting, super-resolution, compressed sensing, high dynamic range imagery, demosaicing. Short introduction to other types of imagery: SAR, Sonar, ultrasound, CT and MRI. Linear and ill-posed restoration problems. |

Moving averages. Finite differences and edge detectors. Gradient, Sobel and Laplacian. Linear translations invariant filters, cross-correlation and convolution. Adaptive and non-linear filters. Median filters. Morphological filters. Local versus global filters. Sigma filter. Bilateral filter. Patches and non-local means. Applications to image denoising. |
Fourier decomposition and Fourier transform. Continuous verse discrete Fourier transform. 2D Fourier transform and spectral analysis. Low-pass and high-pass filters. Convolution theorem. Image sharpening, Image resizing and sub-sampling. Aliasing, Nyquist -Shannon theorem, zero-padding, and windowing. Spectral models of sub-sampling in CT and MRI. Radon transform, k-space trajectories, and streaking artifacts. |

Heat equation. Discretization and finite difference. Explicit and implicit Euler schemes. CFL conditions. Continuous Gaussian convolution solution. Linear and non-linear scale spaces. Anisotropic diffusion. Perona-Malik and Weickert model. Variational methods. Tikhonov regularization by gradient descent. Links between variational models and diffusion models. Total-Variation regularization and ROF model. Sparsity and group sparsity. Applications to image deconvolution. |
Sample mean, law of large numbers, and method of moments. Mean square error and bias-variance trade-off. Unbiased estimation: MVUE, Cramèr-Rao-Bound, Efficiency, MLE. Linear estimation: BLUE, Gauss-Markov theorem, least-square error estimator, Moore-Penrose pseudo-inverse. Bayesian estimators: likelihood and priors, MMSE and posterior mean, MAP. Linear MMSE, applications to Wiener deconvolution, image filtering with PCA, and the non-local Bayes algorithm. Applications to image denoising. |
Limits of Wiener filtering. Non-linear shrinkage functions. Limits of Fourier representation. Continuous and discrete wavelet transforms. Sparsity and shrinkage in wavelet domain. Undecimated wavelet transforms, a trous algorithm. Regularization. Sparse regression, combinatorial optimization and matching pursuit. LASSO, non-smooth optimization, and proximal minimization. Link with implicit Euler scheme. ISTA algorithm. Synthesis versus analysis regularized models. Applications to image deconvolution. |
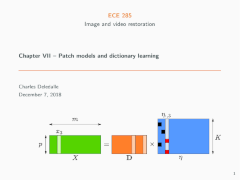
Patch models and sparse decompositions of image patches. Dictionary learning and the k-SVD algorithm. Collaborative filtering and BM3D. Non-local sparse based models. Expected patch log-likelihood. Other applications of patch models in inpainting, super-resolution and deblurring. |
Assignments in Python (individual)
- Assignment 0 - Python, Numpy and Matplotlib (prereq, optional)
- Assignment 1 - Watermarking
- Assignment 2 - Basic Image Tools
- Assignment 3 - Basic Filters
- Assignment 4 - Non-local means
- Assignment 5 - Fourier transform
- Assignment 6 - Wiener deconvolution
- Archive: ece285_IVR_assignments.zip
Projects in Python (pick only one of them, by groups of 2/3)
- Project A - Anisotropic Diffusion
- Project B - Total-Variation
- Project C - Wavelets
- Project D - Non-local regularization
Everything else
- Spring 2019: enroll to Piazza ECE285 MLIP SP19. Access Google Calendar.
Miscellaneaous
- Submitting Notebook to Gradescope as PDF
- Setting up Python and Jupyter with Conda environments on Linux or Max OS-X
- Setting up Python, PyTorch and Jupyter on Windows
- Transferring files from and to an UCSD's DSMLP Pod session
- On the convergence of gradient descent
- Cookbook for data scientists
- Documentation for Git: https://www.atlassian.com/git/tutorials
Last modified: Wed Jan 29 08:57:06 UTC 2020