[français]
FEPLL: Fast EPLL, three ingredients for a 100x speed-up
Description
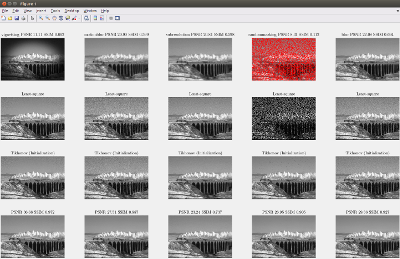 Results of FEPLL
Results of FEPLL
- Image restoration methods aim to recover the underlying clean image from corrupted observations. The Expected Patch Log-likelihood (EPLL) algorithm is a powerful image restoration method that uses a Gaussian mixture model (GMM) prior on the patches of natural images. Although it is very effective for restoring images, its high runtime complexity makes EPLL ill-suited for most practical applications. In this work, we propose three approximations to the original EPLL algorithm. The resulting algorithm, which we call the fast-EPLL (FEPLL), attains a dramatic speed-up of two orders of magnitude over EPLL while incurring a negligible drop in the restored image quality (less than 0.5 dB). We demonstrate the efficacy and versatility of our algorithm on a number of inverse problems such as denoising, deblurring, super-resolution, inpainting and devignetting. To the best of our knowledge, FEPLL is the first algorithm that can competitively restore a 512x512 pixel image in under 0.5s for all the degradations mentioned above without specialized code optimizations such as CPU parallelization or GPU implementation.
- The main contributions of this work are the following. We introduce three strategies to accelerate patch based image restoration algorithms that use a GMM prior. We show that, when used jointly, they lead to a speed-up of the EPLL algorithm by two orders of magnitude. Compared to the popular BM3D algorithm, which represents the current state-ofthe-art in terms of speed among CPU-based implementations, the proposed algorithm is almost an order of magnitude faster. The three strategies introduced in this work are general enough to be applied individually or in any combination to accelerate other related algorithms. For example, the random subsampling strategy is a general technique that could be reused in any algorithm that considers overlapping patches to process images; the flat tail spectrum approximation can accelerate any method that needs Gaussian log-likelihood or multiple Mahalanobis metric calculations; finally, the binary search tree for Gaussian matching can be included in any algorithm based on a GMM prior model and can be easily adapted for vector quantization techniques that use a dictionary.
- We accelerate EPLL by a factor greater than 100 with negligible loss of image quality (less than 0.5dB). This is achieved by combining three independent strategies: a flat tail approximation, matching via a balanced search tree, and stochastic patch sampling. We show that the proposed accelerations are effective in denoising and deblurring problems, as well as in other inverse problems such as super-resolution and devignetting. An important distinction of the proposed accelerations is their genericity: the accelerated EPLL prior can be applied to many restoration tasks and various signalto-noise ratios, in contrast to existing accelerations based on learning techniques applied to specific conditions (such as image size, noise level, blur kernel, etc.) and that require an expensive re-training to address a different problem. Since the speed-up is achieved solely by reducing the algorithmic complexity, we believe that further inclusion of accelerations based on parallelization and/or GPU implementations will allow for real-time video processing. Moreover, the acceleration techniques introduced in this work are general strategies that can be used to speed up other image restoration and/or related machine learning algorithms. For reproducibility purposes, the code of FEPLL is made available below.
Associated publications and source codes
Associated publications/reports:-
Accelerating GMM-based patch priors for image
restoration: Three ingredients for a 100x speed-up,
Shibin Parameswaran, Charles-Alban Deledalle, Loïc Denis, Truong Q. Nguyen
IEEE Transactions on Image Processing (in press)- article IEEE Xplore
- preprint with high image quality (16Mb): pdf
- preprint with poor image quality (8.8Mb): HAL, ArXiv
- article IEEE Xplore
- Download FEPLL:
- Git:
git clone https://github.com/pshibby/fepll_public.git - Archive: master.zip
- GitHub: https://github.com/pshibby/fepll_public
- Git:
Last modified: Fri Aug 23 13:52:00 UTC 2019