NL-InSAR: Non-Local Interferogram Estimator
- Description of the filter
- Qualitative Evaluation of the Denoising Algorithms
- Quantitative Evaluation of the Denoising Algorithms
- Download the NL-InSAR estimator
- References
Description of the filter
- This work has been achieved by Charles Deledalle supervised by Florence Tupin and Loïc Denis. The aim was to adapt the Non-Local means (NL means) filter [7] to InSAR images. The NL-InSAR filter is based on the PPB filter [6] which is an extension of the NL means to non-gaussian noise and multivariate data. Then, an efficient estimator as been designed, able to cope with the statistical nature and the multi-dimensionnality of InSAR images.
- Interferometric synthetic aperture radar (InSAR) data provides reflectivity, interferometric phase and coherence images, which are paramount to scene interpretation or low-level processing tasks such as segmentation and 3D reconstruction. These images are estimated in practice from hermitian product on local windows. These windows lead to biases and resolution losses due to local heterogeneity caused by edges and textures. This paper proposes a non-local approach for the joint estimation of the reflectivity, the interferometric phase and the coherence images from an interferometric pair of co-registered single-look complex (SLC) SAR images. Non-local techniques are known to efficiently reduce noise while preserving structures by performing a weighted averaging of similar pixels. Two pixels are considered similar if the surrounding image patches are "resembling". Patch- similarity is usually defined as the Euclidean distance between the vectors of graylevels. In this paper a statistically grounded patch- similarity criterion suitable to SLC images is derived. A weighted maximum likelihood estimation of the SAR interferogram is then computed with weights derived in a data-driven way. Weights are defined from intensity and interferometric phase, and are iteratively refined based both on the similarity between noisy patches and on the similarity of patches from the previous estimate.
- A full description of NL-InSAR is available in the following report:
Charles-Alban Deledalle, Loïc Denis and Florence Tupin,
NL-InSAR: Non-Local Interferogram Estimation,
IEEE Trans. on Geoscience and Remote Sensing, vol. 49, no. 4, pp. 1441-1452, April 2011
(pdf, bibtex)
- See also: MuLoG filter, PPB filter, NL-SAR.
Qualitative Evaluation of the Denoising Algorithms
(left) Reflectivity, (center) phase difference and (right) coherence of Toulouse (RAMSES, under one meter) ©DGA ©ONERA obtained from top to bottom by the SLC SAR images [1], the 10 iterations of NL-InSAR.
(left) Reflectivity, (center) phase difference and (right) coherence of Resolution test pattern (Synthetic) obtained from top to bottom by the SLC SAR images [1], the 10 iterations of NL-InSAR.
Thanks to the CNES for providing the RAMSES data and to the ANR for providing the TerraSAR-X data in the framework of the EFIDIR project.
Quantitative Evaluation of the Denoising Algorithms
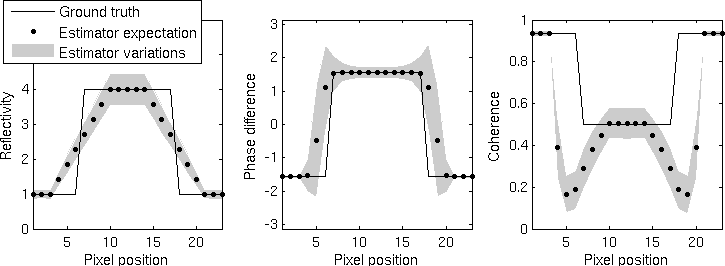
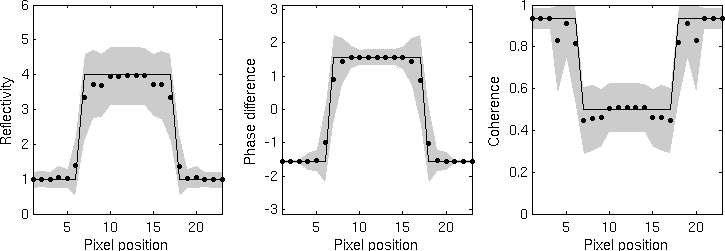
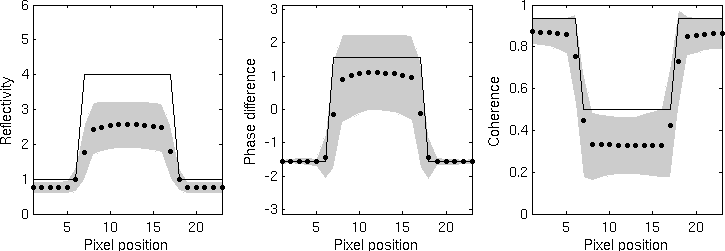
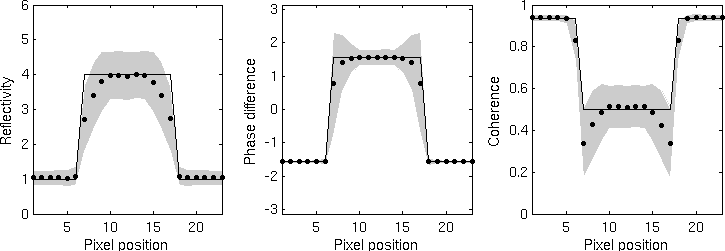
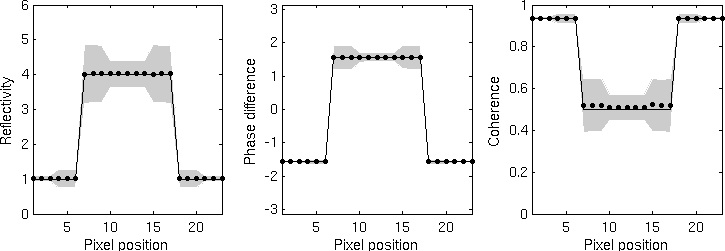
Statistical answer on a rectangular function obtained from top to bottom by the boxcar estimator, Lee's estimator [2], the IDAN estimator [3], the non-iterative NL-InSAR estimator and the (iterative) NLInSAR estimator.
SNR Values of Estimated InSAR Images Using Different Estimators and the Computation Time
| Refl. | Phase | Cohe. | Time (sec) | |
| SLC Images | -2.75 | 3.36 | -1.19 | - |
| WIN-SAR | 5.90 | - | - | 101.76 |
| PEARLS | - | 5.27 | - | 394.83 |
| Boxcar filter | 6.47 | 5.90 | -4.01 | 0.22 |
| Lee | 6.23 | 9.12 | 2.30 | 0.77 |
| IDAN | 5.00 | 7.88 | 0.33 | 522.53 |
| NL-InSAR (non-it) | 6.26 | 8.70 | 5.82 | 148.39 |
| NL-InSAR (10 it.) | 9.02 | 13.04 | 6.92 | 1540.93 |
- To quantify the estimation performances of the NL-InSAR estimator, results obtained on simulated SLC SAR data are given and compared with other estimators. Our NL-InSAR estimator is applied with a search window of size |W| = 21 x 21 and a similarity window of size |Δ| = 7 x 7. The parameters h and T are set as described in [6] which leads to the values h = 12 and T = 0.2|Δ|. A minimum noise reduction of level Lmin = 10 is maintained. We use 10 iterations of the iterative NL-InSAR filter to reach a satisfying estimation. Comparisons have been performed with the classical boxcar filter on a 7 x 7 sliding window, Lee's estimator [2], the IDAN filter with an adaptive neighborhood of maximum size 50 [3] and a non-iterative NL-InSAR with weights based only on the likelihood term with h = 4 (h is lower than in the iterative version to provide a more discriminant likelihood term to compensate the lack of the prior term).
- The figure on the right shows the statistical answer of the five estimators on a cut through a line of width 10. The statistics have been measured on denoised images over 10 000 noisy generated images. The ground truth, the mean and an interval of variation (about 70% of the estimates) is represented on the graphics for the three estimated components. It can be noticed that the boxcar filter is unbiased with a low variance in homogeneous area but it presents a strong spatial bias around the edges of the rectangular function. This spatial bias produces large underestimations of the coherence around edges wich is denoted in [2] as the dark ring effect. Lee's estimator presents less spatial bias but has a higher variance. This is due in part to the edge-aligned windows containing less samples to reduce the variance, but also, to the window selection process which presents high variations. IDAN provides a good restoration of the edges but unfortunately a bias is introduced even in homogeneous area. This is due to the region growing method which tends to lower reflectivity and coherence values [3]. Moreover, the bias increases on the line since the adaptive neighborhood selects samples out of the line. As a result the variance is bigger than the boxcar filter even if there are as many values to estimate the cross-correlation. We assume this phenomenon could be reduced by using a more suitable similarity criterion to define the region growing. NL-InSAR provides the best bias-variance trade-off. Indeed, comparatively to the boxcar filter, Lee's estimator and IDAN, (iterative) NL-InSAR is neither biased in homogeneous area nor around edges. Moreover, its variance is equivalent to the one of the boxcar filter in homogeneous area. NLInSAR has a bigger variance around edges than in homogeneous area since these regions present less redundant patterns. The non-iterative NL-InSAR provides a trade-off between the boxcar filter and the iterative NL-InSAR.
-
To quantify the estimation qualities, the above table presents numerical
results for the resolution test pattern shown on the
previous section.
The performance criterion used is the signal to noise ratio
(SNR):
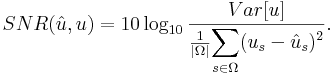
where u is a component of the ground truth image (e.g., the true reflectivity), û its estimate and Ω the image domain. Note that for the interferometric phase, we measure the SNR of the complex phase image ejβ to deal with phase wrapping as proposed in [5]. The results in term of SNR are compared again with the boxcar filter, Lee's estimator, IDAN, the non-iterative NL-InSAR and also with WIN-SAR [4] (a wavelet based amplitude filter) and PEARLS [5] (an adaptive local phase filter). NL-InSAR outperforms all the other filters for all components in term of SNR. In term of computation time, the boxcar filter and Lee's filter provide almost real-time denoising while the others require at least 100 sec to process a 600 x 464 image with an Intel Pentium D 32-bit, 3.20GHz. 10 iterations of NL-InSAR take three times as long as IDAN. If computation time is an issue, non-iterative NL-InSAR is three times faster than IDAN and still provides a better denoising in terms of SNR.

Download the NL-InSAR estimator
These pieces of Matlab softwares are based on C++ Mex-Functions compiled for Linux 32-bit, Linux 64-bit and Windows 32 bit. Matlab script exemples are given, they have been written for MATLAB with the Image Processing Toolbox (to load the images). Please refer to the REAME file for more details. For any comment, suggestion or question please contact Charles-Alban Deledalle at deledalle (at) telecom-paristech (dot) fr.
- NL-InSAR estimator [download],
References
-
M. Seymour and I. Cumming,
Maximum likelihood estimation for SAR interferometry,
In the 1994 International Geoscience and RemoteSensing Symposium., vol. 4, pp. 2272-2274, 1994. -
J. Lee, S. Cloude, K. Papathanassiou, M. Grunes, and I. Woodhouse,
Speckle filtering and coherence estimation of polarimetric SAR interferometry data for forest applications,
IEEE Transactions on Geoscience and Remote Sensing, vol. 41, no. 10 Part 1, pp. 2254-2263, 2003. -
G. Vasile, E. Trouvé , J. Lee, and V. Buzuloiu,
Intensity-Driven Adaptive-Neighborhood Technique for Polarimetric and Interferometric SAR Parameters Estimation,
IEEE Transactions on Geoscience and Remote Sensing, vol. 44, no. 6, p. 1609-1621, 2006. -
A. Achim, P. Tsakalides, and A. Bezerianos,
SAR image denoising via Bayesian wavelet shrinkage based on heavy-tailed modeling,
IEEE Transactions on Geoscience and Remote Sensing, vol. 41, no. 8, pp. 1773-1784, 2003. -
J. Bioucas-Dias, V. Katkovnik, J. Astola, and K. Egiazarian,
Absolute phase estimation: adaptive local denoising and global unwrapping,
Applied Optics, vol. 47, no. 29, pp. 5358-5369, 2008. -
Charles-Alban Deledalle, Loïc Denis and Florence Tupin,
Iterative Weighted Maximum Likelihood Denoising with Probabilistic Patch-Based Weights,
IEEE Trans. on Image Processing, vol. 18, no. 12, pp. 2661-2672, December 2009 (download) - Buades, A. and Coll, B. and Morel, J.M.
A Non-Local Algorithm for Image Denoising,
IEEE Computer Society Conference on Computer Vision and Pattern Recognition, vol. 2, 2005
Last modified: Fri Aug 23 13:52:33 UTC 2019