
Charles Deledalle
Short bio
I am a Research Scientist / Engineer in Machine Learning in the Research and Development Department at Brain Corporation. I received the engineering degree from EPITA and the Master of Science degree from Univ. Paris VI both in France, in 2008. In 2011, I defended my PhD from LTCI, Telecom ParisTech, France, in signal and image processing. I made a postdoctoral fellowship in applied mathematics at CEREMADE, Univ. Paris IX, France, in 2011-2012. I was a CNRS Associate Scientist at IMB, Univ. Bordeaux, France, in 2012-2018, and was on a sabbatical as a visiting professor at UC San Diego in the ECE department from 2017 to 2019. I was the recipient of the IEEE ICIP Best Student Paper Award in 2010, the ISIS/EEA/GRETSI Best PhD Award in 2012, the IEEE GRSS Transactions Prize Paper Award in 2016, and the UCSD ECE Best Lecturer Award in 2019.
[See my resume]
News and calendar
- March 9, 2020. I joined the Research and Development Department of Brain Corporation as a Research Scientist / Engineer in Machine Learning.
- June 6, 2019. I received the UCSD ECE Best Lecturer Award for 2018-2019! For more information about my lectures, please visit this page.
- Dec 13, 2016. I will be a visiting scholar at University California San Diego in the department of Electrical and Computer Engineering from January 1, 2017.
- July 7, 2016. Our former PhD student, Camille Sutour, received both the Aerospace Valley 2016 PhD Award and the University of Bordeaux 2016 "Sciences and Technologies" PhD Award for her thesis in image processing entitled "Numerical night vision system: Automatic restoration and multimodal registration of low light level images".
- April 29, 2016. Our article "NL-SAR: A Unified Nonlocal Framework for Resolution-preserving (Pol)(In)SAR Denoising" (see HAL version) was selected as the winner of the IEEE Geoscience and Remote Sensing Society 2016 Transactions Prize Paper Award!
- April 2, 2016. After four years of research on this topic our paper "The Degrees of Freedom of Partly Smooth Regularizers" has been accepted for publication at the Annals of the Institute of Statistical Mathematics.
- May 18, 2014. Igor Carron has written a post on his blog about our recent paper "Stein Unbiased GrAdient estimator of the Risk (SUGAR) for multiple parameter selection".
- August 28, 2013. Our paper "Non-Local Methods with Shape-Adaptive Patches (NLM-SAP)" has been featured in the most cited articles published since 2011 in International J Mathematical Imaging and Vision.
- Dec 31, 2012. Our paper "Local Behavior of Sparse Analysis Regularization: Applications to Risk Estimation", accepted for publication in Applied and Computational Harmonic Analysis, is now available on-line (pdf, Science Direct (Elsevier)).
- Dec 28, 2012. MooseTeX Beta 1.05 has been released.
- July 6, 2012. I will join l'Institut de mathématiques de Bordeaux (IMB) next autumn.
- June 14, 2012. I have been selected in the competition for a permanent research position at CNRS. I will join a laboratory in mathematics to pursue my research on imaging problems.
- June 14, 2012. Igor Carron has written a post on his blog about our paper "Poisson noise reduction with non-local PCA".
- June 8, 2012. I received the PhD award in Signal, Image and Vision at the 52nd meeting of the EEA Club in Lille (France). This award is jointly delivered by Club EEA, GdR ISIS and GRETSI.
- May 2012. Our recent paper "How to compare noisy patches? Patch similarity beyond Gaussian noise" is featured in the most downloaded articles of the International Journal of Computer Vision with about 900 downloads this last 3 months.
Recent publications
Some of the publications below have appeared in an IEEE journal, Springer journal, Elsevier journal or conference record. By allowing you to download them, I am required to post the following copyright reminder: "This material is presented to ensure timely dissemination of scholarly and technical work. Copyright and all rights therein are retained by authors or by other copyright holders. All persons copying this information are expected to adhere to the terms and constraints invoked by each author's copyright. In most cases, these works may not be reposted without the explicit permission of the copyright holder."

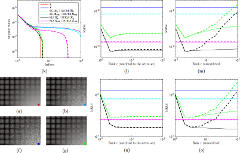
Shibin Parameswaran, Charles-Alban Deledalle, Loïc Denis, Truong Q. Nguyen IEEE Transactions on Image Processing, vol. 28, no. 2, pp. 687-698, 2019 (IEEE Xplore, recommended pdf, HAL, ArXiv) Presented at 5G and Beyond forum, May 2018, La Jolla, CA, USA (poster) Image restoration methods aim to recover the underlying clean image from corrupted observations. The Expected Patch Log-likelihood (EPLL) algorithm is a powerful image restoration method that uses a Gaussian mixture model (GMM) prior on the patches of natural images. Although it is very effective for restoring images, its high runtime complexity makes EPLL ill-suited for most practical applications. In this paper, we propose three approximations to the original EPLL algorithm. The resulting algorithm, which we call the fast-EPLL (FEPLL), attains a dramatic speed-up of two orders of magnitude over EPLL while incurring a negligible drop in the restored image quality (less than 0.5 dB). We demonstrate the efficacy and versatility of our algorithm on a number of inverse problems such as denoising, deblurring, super-resolution, inpainting and devignetting. To the best of our knowledge, FEPLL is the first algorithm that can competitively restore a 512x512 pixel image in under 0.5s for all the degradations mentioned above without specialized code optimizations such as CPU parallelization or GPU implementation. |
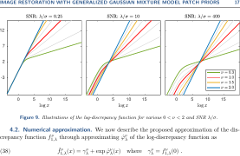
Charles-Alban Deledalle, Shibin Parameswaran, Truong Q. Nguyen SIAM Journal on Imaging Sciences, vol. 11, no. 4, pp. 2568-2609, 2018 (epubs SIAM, HAL, ArXiv) Presented at LIRMM Seminar, Jan 2019, Montpellier, France (slides) Patch priors have become an important component of image restoration. A powerful approach in this category of restoration algorithms is the popular Expected Patch Log-likelihood (EPLL) algorithm. EPLL uses a Gaussian mixture model (GMM) prior learned on clean image patches as a way to regularize degraded patches. In this paper, we show that a generalized Gaussian mixture model (GGMM) captures the underlying distribution of patches better than a GMM. Even though GGMM is a powerful prior to combine with EPLL, the non-Gaussianity of its components presents major challenges to be applied to a computationally intensive process of image restoration. Specifically, each patch has to undergo a patch classification step and a shrinkage step. These two steps can be efficiently solved with a GMM prior but are computationally impractical when using a GGMM prior. In this paper, we provide approximations and computational recipes for fast evaluation of these two steps, so that EPLL can embed a GGMM prior on an image with more than tens of thousands of patches. Our main contribution is to analyze the accuracy of our approximations based on thorough theoretical analysis. Our evaluations indicate that the GGMM prior is consistently a better fit for modeling image patch distribution and performs better on average in image denoising task. |
Jérémie Bigot, Charles Deledalle, Delphine Féral Journal of Machine Learning Research, vol. 18, no. 137, pp. 1-50, 2017 (JMLR, ArXiv) Presented at ISNPS'2018, June, Salerno, Italy (slides) We consider the problem of estimating a low-rank signal matrix from noisy measurements under the assumption that the distribution of the data matrix belongs to an exponential family. In this setting, we derive generalized Stein's unbiased risk estimation (SURE) formulas that hold for any spectral estimators which shrink or threshold the singular values of the data matrix. This leads to new data-driven shrinkage rules, whose optimality is discussed using tools from random matrix theory and through numerical experiments. Our approach is compared to recent results on asymptotically optimal shrinking rules for Gaussian noise. It also leads to new procedures for singular values shrinkage in matrix denoising for Poisson-distributed or Gamma-distributed measurements. |
[All] [Scholar Google]
Last modified: Thu Mar 12 05:15:57 Europe/Berlin 2020
This website uses Google Analytics [know more]